Recently a friend of mine expressed an interest in knowin g what the equation was for the night/day line on a rectangular map of the earth. For example:
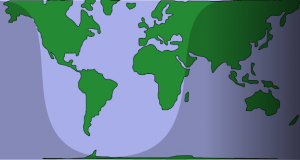
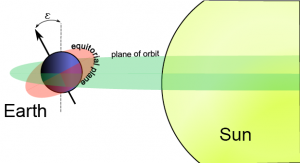
The line of night is generated by a projection of the Sun's light onto the Earth, which we will consider to be a perfect spheroid with semi-major axis of $latex R_1$ and semi-minor axis of $latex R_2$. If viewed from the "side" the line of night will appear to be a line with slope equal to that of the axial tilt (a.k.a obliquity) of earth. This is the inclination angle of Earth's planetary rotation axis in relation to its orbital plane, usually denoted by $latex \epsilon$
A typical map of the earth is a projection from spherical coordinates onto a cylindrical plane. This is done by drawing a rectangular image where the latitude ($latex \lambda$) is mapped to the x-axis and the longitude ($latex \phi$) is mapped to the y-axis (contrary to the coordinate system used by the digital imaging industry, here we describe the origin as being in the center of the image, with the positive x-axis being to the right, and positive y-axis being up).
Consider then a plane that is perpendicular to the earth's plane of orbit, and perpendicular to the vector pointing from the center of the earth toward the sun, and that intersects the earth at it's center. The line of night is the intersection of this plane with the Earth. From this observation we can develop an equation for the line of night in terms of $latex \phi$ and $latex \lambda$.
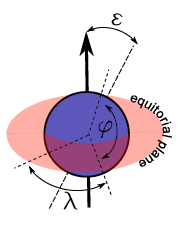
[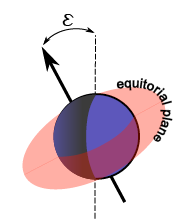
If we place a coordinate system on the surface of the earth, centered at the intersection of the line of night with the equator with the positive x-axis corresponding to positive $latex \lambda$ and positive y-axis corresponding to positive $latex \phi$ we can describe the line-of-night plane as
$$y = s x$$
where the slope $latex s$ is related to the obliquity as
$$ s = \frac{1}{\tan(\epsilon)} $$
where $latex \epsilon$ is the inclination of the axial tilt of the Earth's axis at solstice ($latex \epsilon_0$) scaled according to the position of the Earth in it's orbit
$$ \epsilon = \epsilon_0 \cos( \frac{day}{360} ) $$
The inclination of the earth's axis at solstice is $latex \epsilon_0 = 23.5^\circ $
From the parameterization of a spheroid, we know that
$$ x = R_1 \sin( \lambda ) \cos( \phi ) $$
$$ y = R_2 \sin( \phi ) $$
Combining these with the equation above for the line-of-night plane we see that
$$ y = \frac{1}{\tan( \epsilon )} x $$
$$ R_2 \sin( \phi ) = \frac{1}{\tan( \epsilon )} R_1 \sin( \lambda ) \cos( \phi ) $$
$$ \tan( \phi ) = \frac{1}{\tan( \epsilon )} \frac{R_1}{R_2} \sin( \lambda ) $$
$$ \phi = \text{tan}^-1 \left( \frac{1}{\tan( \epsilon )} \frac{R_1}{R_2} \sin( \lambda ) \right) $$
Plotting the value of the longitude against latitude over a range of axial inclinations from $latex \epsilon = 0$ to $latex \epsilon = 23.5^\circ$, and assuming $latex R_1 = R_2$ results in the following:
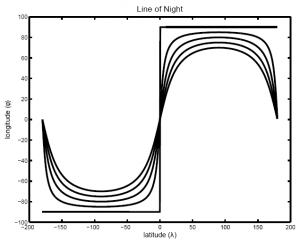
Which has exactly the shape we were looking for.

Commentaires
Comments powered by Disqus