I was looking around today for an algorithm for In-Place Matrix Transposition and didn't manage to find anything, so this is what I came up with. I'll analyze and document it fully later, but I just wanted to get it down.
It's wasteful in that it will repeat a lot of operations, especially for "thin" matrices (worst case: vector). But it will work, never-the-less. Worst case run time is at most $latex O(n^2)$ where $latex n$ is the size of the matrix $latex n = rows times columns$
Edit: No longer arbitrarily repeating cycles ( was leading to identity operation, duh! ).
template void CMatrix::inPlaceTranspose( ) { using std::swap; resize(cols,rows); int i, j, k, k_start, k_new; int n = rows; int m = cols; int length = rows*cols; for(k_start=1; k_start < length; k_start++) { T temp = data[k_start]; bool abort = false; k_new = k = k_start; // go through the cycle once and ensure that the starting point is // minimal do { if( k_new < k_start ) { abort = true; break; } k = k_new; i = k%n; j = k/n; k_new = i*m + j; }while(k_new != k_start); // if the current value is not the minimum of the cycle, then don't // perform the cycle if(abort) continue; // otherwise, perform the cycle k_new = k = k_start; do { swap( data[k_new], temp ); k = k_new; i = k%n; j = k/n; k_new = i*m + j; }while(k_new != k_start); swap( data[k_new], temp ); } }
And the result: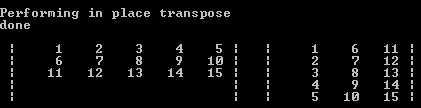

Commentaires
Comments powered by Disqus